Visitas: 4
Joaquín Díaz Atienza
DEFINICIÓN
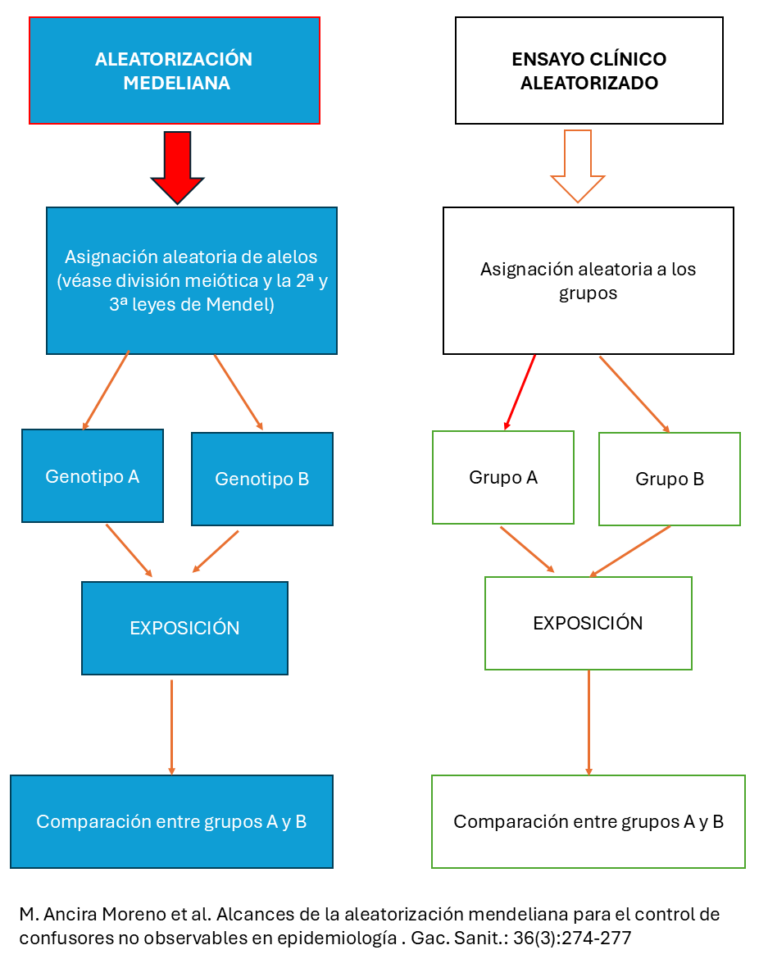
El modelo estadístico de aleatorización medeliana es un caso particular del modelo de variable instrumental. Metodológicamente se pretende obtener las mismas posibilidades que presentan los ensayos clínicos aleatorizados en el establecimiento de realaciones de causa/efecto y controlar los sesgos de confusión propios de los diseños de casos y controles y cohortes. En definitiva, garantizar que los sujetos sean asignados aleatoriamente a los diferentes grupos en estudio.
BASES DE LA ALEATORIZACIÓN MENDELIANA
A continuación presento dos gráficos sobre los pasos a seguir en los diseños de aleatorización medeliana (AM, en adelante) y en los ensayos clínicos aleatorizados (ECA, en adelante):
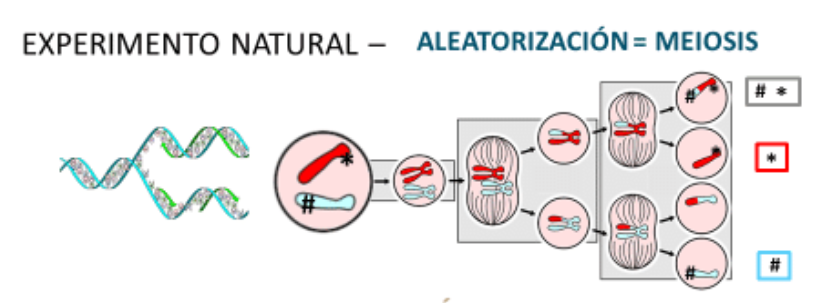
Figura 1. Árbol de decisión en la AM y los ECA1
El modelo de AM tiene su origen en la segunda y tercera leyes de Mendel. La segunda, hace referencia a la segregación de los alelos que nos dice la manera en la que los alelos de un gen se distribuyen en los gametos durante la meiosis. La segragación nos asegura la dirección de la causalidad. La tercera, hace referencia a la asignación independiente de los mismos. La asignación independiente nos asegura la aleatorización. Durante la fecundación, cada gamento se une dando lugar al cigoto que pasa a ser diploide. Cada gamento aporta la mitad del ADN de la madre y la otra mitad del padre.
Estos fenómenos biológicos brindan la posbilidad de que las variantes genéticas puedas ser untilizadas como variables instrumentales, ya que cumplen las siguientes características:
- La VI debe tener una relación cuantificable con el factor de exposición .
- No puede estar relacionada dierectamente con el resultado, solo puede estarlo a través de factor de exposición.
- Debe ser independiente de los factores de confusión, conocidos y no conocidos (no controlables) que puedan existir entre la exposición y el resultado.
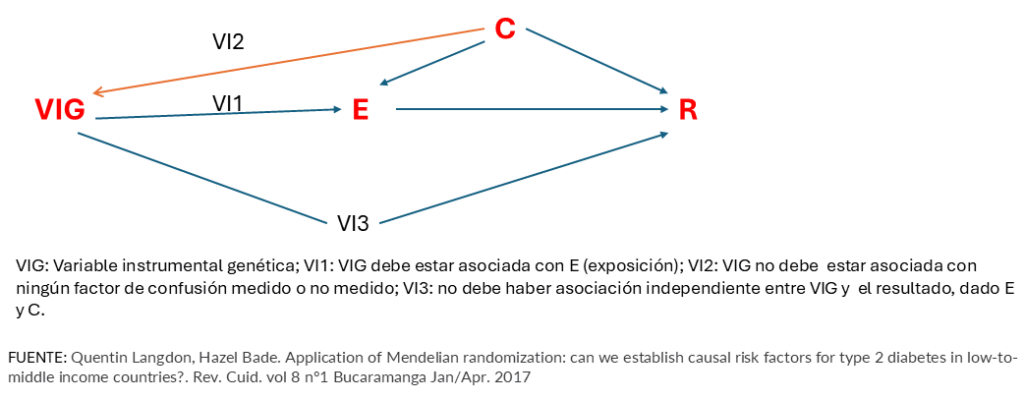
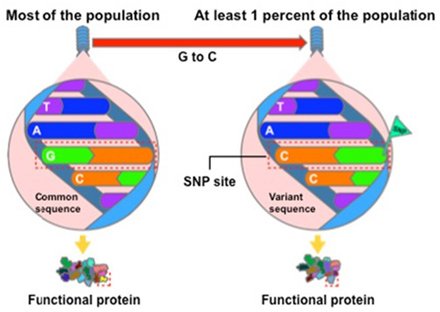
La representación gráfica de las carecaterísticas mencionadas suele hacerse a través de los denominados gráficos acíclicos dirigidos (Figura 2)
Figura 2. Gráfico acíclico dirigido sobre las características de una VI genética2
El primer supuesto de la VIG debe apoyarse en la evidencia científica previa. El segundo se apoya en el análisis de las posibles relaciones de la VIG con los confusores (tanto exógenos, como endógenos), siempre que sea posible conocerlos. Para el tercero debemos evaluar la posibilidad de que la VIG afecte de forma independiente al resultado sin que sea a través de la exposición.
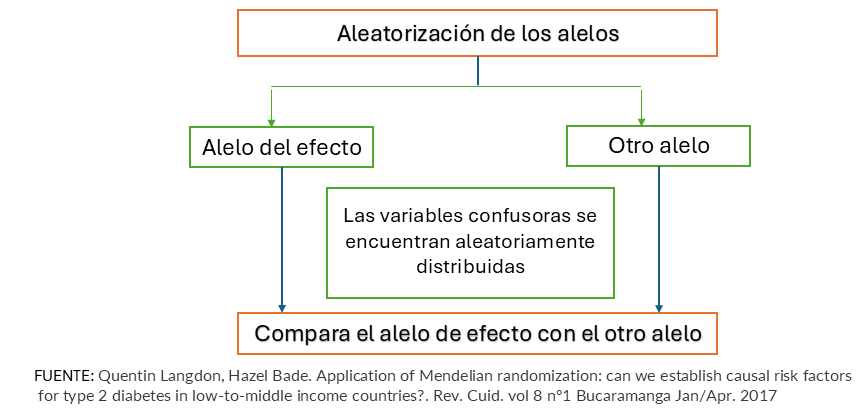
Nuevamente, Quintín Langdon y Hazel-Bade nos presentan un gráfico bastante explicativo del procedimiento que se sigue en un Modelo de Aleatrización Medeliana (Figura 3):
LIMITACIONES DE LA AM (M. Ancira-Moreno et al)
Las limitaciones de la AM están relacionadas con la violación de los tres supusetos que debe cumplir toda variable instrumental y que hemos eplicado anteriormente.
Variable instrumental débil
Una variable instrumentales considerada débil, si a realizar una regresión de la exposición con la VM presenta un valor del estadístico F<10. Cuando nos enfrentamos a este supuesto se propone como solución la utilización de varias variables genéticas instrumentales. También se ha propuesto realizar el diseño de un instrumento de puntuación combinando varias instrumentales: sería el denominado «puntaje alélico o puntaje de riesgo genético«. ponderado o no ponderado. El poder estadístico de las puntuaciones de alelos se puede incrementar ponderando cada variante por el tamaño de su asociación con el factor de exposición.
También se le denomina «sesgo instrumental débil» y puede suceder cuando se utilizan «una o mas variantes genéticas que explican una pequeña proporción de la variación en el factor de riesgo». Suele presentarse en muestras de estudio pequeñas.3
2. Estratificación de la población
La indiscutible variabilidad con la que sucede la relación entre el alelo y la enfermedad o bien la tasa de exposicón entre diferentes grupos humanos (étnicos), hace que la mayoria de los expertos nos recomienden realizar análisis estratificados para evitar factores de confusión respecto a la asociación. Existe numerosos ejemplos en la literatura médica en los que se han cometido este tipo de errores.
- Desequilibrio de ligamento
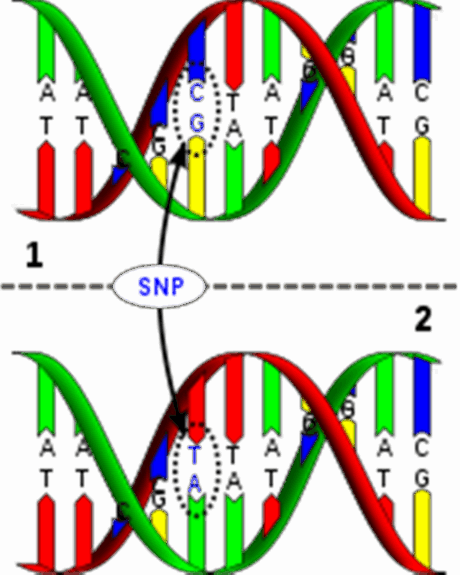
El desequilibrio de ligamiento se refiere a la existencia no aleatoria de alelos en diferentes loci que están cercanas entre sí en el mismo cromosoma y que generalmente se heredan juntas. La frecuencia de asociación de sus diferentes alelos es mayor o menor que lo esperado por azar. Esta puede afectar a la necesaria aleatorización mendeliana. Sin emabargo, no suele verse afectada cuando se utiliza una sola variante genética por gen.
Canalización
Es un proceso mediante el cual se produce una compensación en la función y en la estructura de los tejidos. Esto se debe a la existencia de variantes genéticas adaptativas que podrían activarse con la finalidad de conseguir la homeostasis, ante las deficiencias en los genes que le corresponden ejecutar esta función.
Por supesto, la relación genotipo/enfermedad podría verse afectada por la existencia de estas variantes genéticas adaptativas.
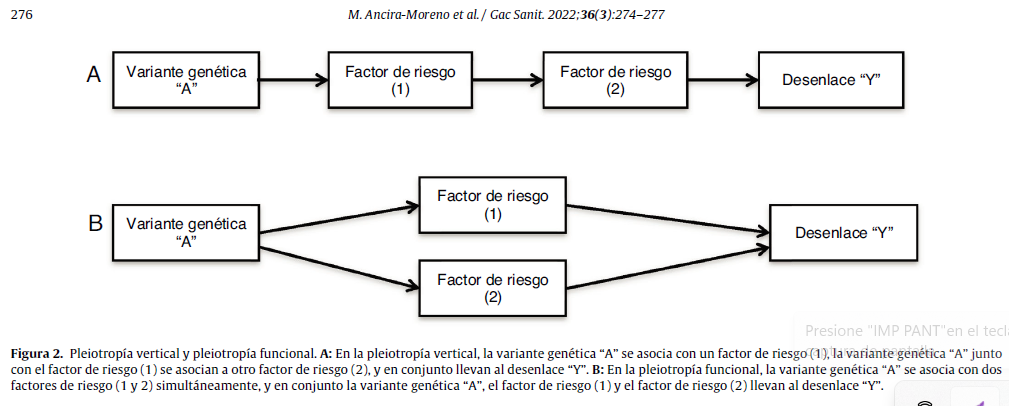
Efectos pleiotrópicos
La realidad es que son numerosas las variantes genéticas que se asocian con múltiples factores de riesgo. Es decir, sería la participación de una variante genética en múltiples vías biológicas. Se le denominan efectos pleiotrópicos. Suelen dividirse en pleiotropía vertical (cuando se afectan otros rasgos a través del factor de riesgo de interés en nuestra ivestigación) y pleiotropía horizontal ( cuando afecta el resultado a través de otro rasgo diferente al que se está investigando). Ambos efectos pueden estar presentes simultáneamente. Para establecer la estimación de causalidad, se asume que factor de riesgo es causalmente indepediente.
La pleitropía horizontal es una violación de las características exigidas a la variable instrumental ya que el resultado no se produce exclusivamente a través del factor de riesgo. La pleiotropía vertical no afecta especialmente ya que, en definitiva, lo que nos muestra es que un determinado factor influye en el resultado (Davies et al, 2018).
En la figura 4 presentamos gráficamente los dos modelos de pleiotropía vertical y horizontal (Ancira-Moreno et al, 2022)
ANALÍSIS ESTADÍSTICOS: FORTALEZAS Y LIMITACIONES4
No es cometido de este artículo entrar en detalle en los diferentes métodos estadísticos utilizados en las investigaciones que emplean la aleatorización mendeliana. El cuadro resumen que realizan Hemani et al(2018) es bastante explicativo sobre los complejos procedimientos que se requieren para anular los variados sesgos que pueden producirse con este método. Para aquellos que deseen profundizar le recomendamos su lectura.
Cuadro 1
- Aleatorización mendeliana (AM) de un solo instrumento (VI), para un sola hipótesis o sin hipótesis
| Estrategia | Descripción | Limitaciones |
Colonización genética:
| Utilizar la co-localización genética para eliminar la posibilidad de variantes causales distintas; si hay VI disponibles para el resultado, entonces probar el efecto causal inverso; si no, utilizar AM Steiger; utilizar análisis basado en mediación genética para intentar separar la pleiotropía horizontal y vertical.
| La potencia estadística puede ser baja y los métodos de la AM no pueden distinguir la pleiotropía vertical de la horizontal. Los métodos basados en mediación genética son susceptibles de errores de medición, factores de confusión y requieren datos individuales. AM-RAPS (1) requiere la selección requiere la slección de instrumentos o VI, la estimación del efecto de la exposición del SNP (2) y la estimación del efecto en el resultado del SNP a partir de muestras independientes |
| (1) AM-RAPS: Robust Ajusted Profil Score; (2) SNP: Polimorfismo de un solo nucleótido; AM: aleatorización mendeliana |
Cuadro 2
b. Análisis de hipótesis única con múltimples VI (instrumentos)
| Estrategia | Descripción | Limitaciones |
Efectos aleatorios IVW (1) o MR-RAPS:
| Comience con el modelo más simple y luego pruebe la heterogeneidad; si hay heterogeneidad, realice análisis de sensibilidad.
| El poder de la prueba de heterogeneidad es bajo; no es una prueba basada en principios para decidir la confiabilidad del resultado; el uso de muestras de control negativo requiere datos a nivel individual y la disponibilidad de una interacción GxE o GxG apropiadas. |
| Marco de Rucker (2) | Utilice las estadísticas de heterogenidad Q y Q’ (3) para navegar entre cuatro modelos diferentes de pleiotropía horizontal. | Restringido a modelos específicos de pleiotropía horizontal y su pode estadístico decae sustancialmente cuando el modelo pleiotrópico aumenta su complejidad. |
| Promedio del modelo bayesiano | Promedio de tres modelos diferentes de pleiotropía horizontal | Como se indico anteriormentees díficl tomar una decisión si la distribución posterior es multimodal. |
| (1) IVW: Ponderado por la varianza inversa; (2) Marco deRucker: Método estadístico que valora la heterogenidad. Primero se estima el análisis de los efectos fijos IVW y luego el estadístico Q de Cochran para la heterogeneidad. Estadístico Q’: Q’ de Rucker. |
Cuadro 3
c. Análisis de la exposición sin hipótesis con múltiples instrumentos (VI)
| EEstrategia | DeDescripción | LLimmitaciones |
| Efectos aleatorios IVW o AM-RAPS. Seguimiento utilizando la sección B
Estimación del modo ponderado
AM-MoE (1)
| Utilice un método único para identificar posibles asociaciones y luego contnúe con una estrategia de la sección B.
Utilice un solo método para todas las pruebas. Las simulaciones sugieren el máximo rendimiento en términos de alta potencia y baja FDR(2) con un solo método. Continúe con una estrategia la sección B. Utlice el aprendizaje automático (1) para seleccionar la estimamación de cada prueba. Continúe con uan estrategia de la sección B. | Mayor pontencia pero probablemente también la tasa más alta de de falsos descubrimientos; AM-RAPS requiere que la exposición y el resultado no tenga superposición de las muestras, lo que puede ser difícil de probar.
No se puede estimar el patrón de ancho de banada.
Potecialmente más lento de ejecutar, no brinda información sobre por qué se eligió un método en particular. |
| (1)AM-MoE: Se denomina mezcla de expertos y es un marco de aprendizaje automático en el que los datos pueden ser alimentados a varios métodos diferentes («expertos») y luego se selecciona el más confiable de ellos. (2) FDR: Tasa de falsos descubrimientos |
ARTÍCULO ANTERIOR:
ARTÍCULO SIGUIETE
BIBLIOGRAFÍA
- M. Ancira-Moreno et al. Alcances de la aleatorización mendeliana para el control de confusores no observables en epidemiología. Gac. Sanit.; 36(3): 274-277. DOI:10.1016/j.gaceta.2021.01.008 [↩]
- Quentin Langdon, Hazel Bade. Application of Mendelian randomization: can we establish causal risk factors for type 2 diabetes in low-to-middle income countries?. Rev. Cuid. vol 8 nº1 Bucaramanga Jan/Apr. 2017.DOI: https://doi.org/10.15649/cuidarte.v8i1.373 [↩]
- Davies NM, Holmes, MV y cols. Reading Mendelian Randomisation studies: a guide, glossary, and checklist for clinicians. BMJ 2018; 362. DOI: https://doi.org/10.1136/bmj.k601 [↩]
- Hemani G, Bowden, J et al. Evaluating the potencial rol of pleiotropy in Mendelian randomisation studies. Mol Genet. 2018 May 16; 27(R2):R195-R208. DOI: 10.1093/hmg/ddy163 [↩]